Первая серия задач
1.1 Для десятичной записи некоторого числа использованы только цифры 0, 3 и 9. Докажите, что если количество троек при этом равно 2005, то число не может быть квадратом.
1.2 Восстановите исходный текст и опишите ход дешифровки.
ЭШЧПЯА ТЯ РСНСУХСЭ
ЭСОКЧЖЯБОГ Ч
ОСХПМЗЯБОГ ЗФБ
НЯЦТДЦ РПЧЭЪН
СЫТСУМ ЧШ УСЧК
РСОФЪЫСЭЯНЪФЪЦ
ФЪСТЯПЫС ЫЯ ЭЧТИЧ
1.3 Положим f(1) = 1 и через f(n) обозначим количество вхождений числа n в неубывающую последовательность натуральных чисел:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... |
| f(n) | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | ... |
1) Выпишите следующие десять значений функции f(n).
2) Составьте программу для вычисления этой функции.
3) Найдите явный вид функции f(n).
1.4 Даны вычисления на одном из европейских языков:
fem * fir = tyve
fem * fem = femotyve
fireofirsinstyve + seks = halvfemsinstyve
seksotresinstyve + niden = femofirsinstyve
femden + femotresinstyve = firsinstyve
treden + = niotyve
seks * ni =
niotresinstyve + fireotyve =
Заполните пропуски.
1.5 Марсиане бывают трех-, пяти- или двенадцатирукими. Некоторое число марсиан, представляющих все указанные разновидности, выполнили призыв "Возьмемся за руки, друзья!" таким образом, что каждый оказался соединенным с любым другим не более чем одной рукой и все руки при этом были заняты.
1) Опишите одну из возможных конструкций.
2) Каково наименьшее возможное число участников такого хоровода?
Вторая серия задач
2.1 Палиндромом называют число, не изменяющееся от направления его прочтения "слева - направо" или "справа - налево". Докажите, что не существует четырехзначных палиндромов, являющихся простыми числами.
2.2 В шифре Виженера ключом является последовательность неотрицательных целых чисел k=(k1, k2, ..., kn). Шифрование производится следующим образом: открытый текст разбивается на блоки длины n (последний блок может быть неполным) и в каждом из них i-я буква циклически сдвигается по алфавиту на ki позиций вправо, 1<=i<=n. Расшифруйте следующую полученную методом Виженера криптограмму, зная, что в открытом тексте (без знаков препинания и пробелов) наиболее частыми буквами являются И, Н, Е, О, А, Б (в порядке неубывания частот).
фоявчбсрщмнтэттезнфуйырзбгацуплбэфлдщнобншфецзьншиувнфссдоъяысдцумсбчетнс
бэфлдщногрягулыкзноабнтюекфчрлбэфлдщноюхнюкьщнаьояытяэлчшшэюзчарэнлтькмщы
тяытеичылятденндъртцйъфбавтзщагрчююссхрятеябблфлаечзоычыжньньгулфлацемибе
шшснлтькмщыйыцсиегщхгвеюыжньньхувмущддснлтькмщыюыхнювадъъфбавтзнуцзчммрчл
кмисобелфбаьнзшиуяееснярнжпнтбтъсзтгхяодеыжнфхчечщвавечбьнчхкрщоч
2.3 В качестве первого члена последовательности берется произвольное натуральное число, кратное трем. Далее за любым членом последовательности следует сумма кубов всех его цифр.
1) Каким общим свойством обладают такие последовательности?
2) Докажите это свойство (возможно используя компьютер).
2.4 Даны словосочетания на одном из памирских языков с их переводами на русский язык.
КУЗАА ХАЦ - кувшин воды
ЧАЛАК ЗИМААДЬ - ведро земли
ТАМБАЛ БЮЮН - борода бездельника
БИИГ ДЮЮНАА - горшок зерна
КУЗАА ГЪЭВ - крышка кувшина
БЕЕЧОРАА ЗИМААДЬ - земля бедняка
Сделайте обратный перевод для ведро воды, зерно бедняка, кувшин бездельника.
2.5 Набор диагоналей правильного n-угольника называется максимально плоским, если никакие две диагонали из этого набора не пересекаются и присоединение к нему любой другой диагонали нарушает это свойство. Сколько существенно различных максимально плоских наборов диагоналей имеет
1) 12-угольник?
2) 13-угольник?
3) n-угольник?
(Два набора считаются существенно различными, если их нельзя совместить как геометрические фигуры).
Третья серия задач
3.1 “Квадратное уравнение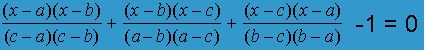
имеет три различных корня: a, b и c.” В чем здесь дело?
3.2 В таблице 4x4 вырезаны 4 клетки и в них вписаны первые 4 буквы открытого текста – слева направо и сверху вниз. Затем решетка поворачивается на 90 градусов и в прорези вписываются следующие 4 буквы. Этот процесс повторяется еще два раза. Из заполненной таблицы буквы считываются по столбцам:
ТРДЕПЖИЯЗСНГОАЕЕ.
1) Расшифруйте криптограмму.
2) Объясните, почему секретный ключ (т.е. решетка) был закодирован шифровальщиком и передан получателю как 3114.
3.3 Последовательность натуральных чисел a1, a2, ..., an называется цикличной, если сумма собственных делителей (т.е. делителей числа, отличных от него самого) числа ai равна числу ai+1, 1 <= i <= n-1, а сумма собственных делителей числа an равна a1. Составьте программу, которая выведет все цикличные последовательности из диапазона от A до B, 0< A < B <106.
3.4 Некто пытается подобрать пароль к серверу методом “грубой силы” (последовательного перебора). Он знает, что пароль назначается компьютером, регулярно меняется, а предыдущие пароли выглядели следующим образом (все буквы - латинские):
abStwdRd
pVtrKRLp
iryzhToz
URbhhbEH
OJEXHZmJ
pzTDXJrZ
Какие выводы надо сделать, чтобы ускорить процесс подбора пароля?
3.5 (Гамильтонова цепь).
Дан правильный многоугольник со всеми его диагоналями. Докажите, что если каким-то образом ориентировать каждую сторону и каждую диагональ, то, отправляясь из некоторой вершины и двигаясь по отрезкам в заданных на них направлениям, можно посетить все другие вершины точно по одному разу.
Четвертая серия задач
4.1 В таблицу m x n вписываются все целые числа от 1 до mn таким образом, что в каждой строке и в каждом столбце числа идут в возрастающем порядке (в строке слева направо, в столбце – сверху вниз). Придумайте такой способ заполнения таблицы, при котором сумма чисел в заданном столбце будет
1) максимальной,
2) минимальной.
4.2 Восстановите три слова, утраченные при передаче шифровки.
А БВГД, ЕГЕ ЖЗИГЙК БГЛГМН.
А ОЕПЖП ЖЗИН ЗЗ. ЕЙП ЖЗИГЗЙ БГЛГМР ОЕПЖЗЗ,
ЙПЙ ЖЗИРЙ СПТКИЗ БГЛГМ. БГ ЕГУЛНД
. . . . . . . . . . . . . . . . . . . . . . . . . ПМЕР.
4.3 (Разделение секрета)
Каждый из трех хранителей Печати A, B, C имеет свой секретный ключ – некоторое только ему известное число, соответственно a, b, c. Чтобы открыть сейф, где находится Печать, необходимо найти значение f(a, b, c), где f – специально назначаемая для каждой такой акции функция. Сегодня наступил один из редких торжественных дней, и утром было сообщено, что f(x, y, z) = xyz. Составьте протокол (пошаговую последовательность действий участников), после выполнения которого A, B, C смогут открыть сейф, сохраняя в тайне свои личные ключи.
4.4 Используя цифры 1, 2, 3, 4, 5, напишите число, не содержащее в своем составе двух равных подряд идущих чисел, и такое, что при приписывании справа любой из заданных цифр указанное свойство нарушается.
4.5 В условиях задачи 3.5 докажите, что существует вершина, из которой до любой другой вершины можно добраться самое большее за два шага.







